[2015 개정 교육과정]중3 수학(하)

 

 

Ⅴ. 삼각비

1. 삼각비의 뜻

 

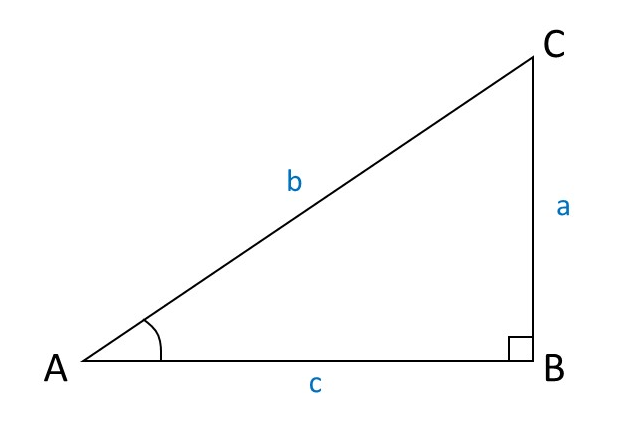
①삼각비

  -$\sin A={\displaystyle \frac{a}{b}}$

  -$\cos A={\displaystyle \frac{c}{b}}$

  -$\tan A={\displaystyle \frac{a}{c}}$

 

 

 

 

 

 

 

②삼각비의 값

	$0˚$	$30˚$	$45˚$	$60˚$	$90˚$
$\sin A$	0	${\displaystyle \frac{1}{2}}$	${\displaystyle \frac{\sqrt{2}}{2}}$	${\displaystyle \frac{\sqrt{3}}{2}}$	1
$\cos A$	1	${\displaystyle \frac{\sqrt{3}}{2}}$	${\displaystyle \frac{\sqrt{2}}{2}}$	${\displaystyle \frac{1}{2}}$	0
$\tan A$	0	${\displaystyle \frac{\sqrt{3}}{3}=\frac{1}{\sqrt{3}}}$	1	${\displaystyle \sqrt{3}=\frac{\sqrt{3}}{1}}$	한없이 길어짐

 

③삼각비의 표

2. 삼각비의 활용

①길이 구하기

②넓이 구하기

  -삼각형(두변 a, c와 그 끼인각 B의 크기를 알 때): $△ABC={\displaystyle \frac{1}{2}ac·\sin B}$

  -평행사변형(이웃하는 두 변 a, b와 그 끼인각 B의 크기를 알 때): $\square ABCD=ab·\sin B$

  -사각형(두 대각선 a, b와 두 대각선이 이루는 각 x의 크기를 알 때): $\square ABCD={\displaystyle \frac{1}{2}ab·\sin x}$

 

 

 

Ⅵ. 원의 성질

1. 원과 직선

①원

  -원의 중심에서 현에 내린 수선은 그 현을 이등분한다.

  -현의 수직이등분선은 원의 중심을 지난다.

  -중심으로부터 같은 거리에 있는 현의 길이는 같다.

  -길이가 같은 두 현은 원의 중심으로부터 같은 거리에 있다.

  -원의 접선은 그 접점을 지나는 원의 반지름에 서로 수직이다.

  -반지름과 원이 만나는 점에서 반지름에 수직으로 그은 직선은 그 원의 접선이다.

  -원 밖의 한 점에서 원에 그을 수 있는 접선은 2개이며, 두 접선의 길이는 같다.

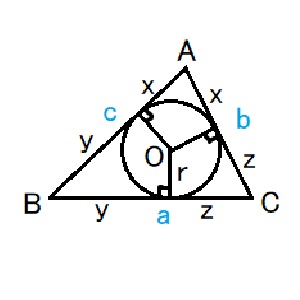
②삼각형의 내접원

  -(길이) $a+b+c+=2(x+y+z)$

  -(넓이) $△ABC={\displaystyle \frac{1}{2}r(a+b+c)}$

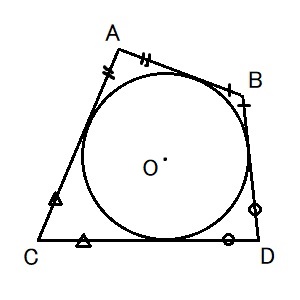
③원에 외접하는 사각형

  -(길이) $\overline{AB}+\overline{CD}=\overline{AD}+\overline{BC}$

  -두 쌍의 대변의 길이의 합은 서로 같다.

2. 원주각의 성질

①원주각

  -한 호에 대한 원주각의 크기는 그 호에 대한 중심각의 크기의 ${\displaystyle \frac{1}{2}}$ 이다.

  -한 호에 대한 원주각의 크기는 모두 같다.

  -반원에 대한 원주각의 크기는 90˚이다.

  -원주각의 크기와 호의 길이는 정비례한다.

  -두 점 C, D가 직선 AB에 대하여 같은 쪽에 있을 때, ∠C =∠D이면, 네 점 A, B, C, D는 한 원 위에 있다.

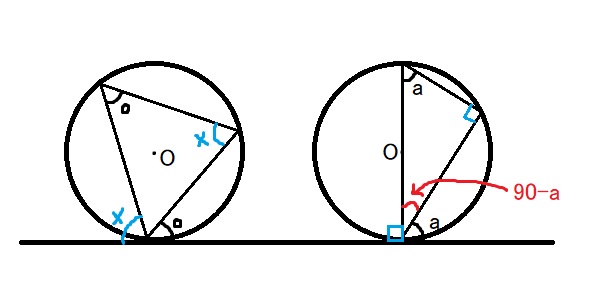
  -원의 접선과 현이 이루는 각의 크기는 호에 대한 원주각의 크기와 같다.

  -두 원의 공통인 접선일 때, 동위각, 엇각의 크기가 같은 두 직선은 평행하다.

②원에 내접하는 사각형

  -한 쌍의 대각의 크기의 합은 180˚이다.

  -한 외각의 크기는 그 외각에 이웃한 내각에 대한 대각의 크기와 같다.

 

 

 

Ⅶ. 통계

1. 대푯값과 산포도

①대푯값: 평균, 중앙값, 최빈값 등

  -중앙값(홀수): ${\displaystyle \frac{n+1}{2}}$번째 값

  -중앙값(짝수): ${\displaystyle \frac{n}{2}}$번째 값과 ${\displaystyle \frac{n}{2}+1}$번째 값의 평균

②산포도: 변량들이 흩어져 있는 정도를 하나의 수로 나타낸 값으로, 분산, 표준편차 등

  -(편차) = (변량) - (평균)

  -(분산) = ${\displaystyle \frac{(편차{)}^2의총합}{(변량의개수)}}$ 

  -(표준편차) = $\sqrt{(분산)}$

  -분산 또는 표준편차가 작을수록 평균을 중심으로 모여있는데, 이를 자료의 분포가 고르다고 함

2. 상관관계

①산점도: 두 변량 사이의 관련성을 알아보기 위하여 순서쌍 $(x,y)$를 좌표평면에 나타낸 그래프

②상관관계

  -양의 상관관계

  -음의 상관관계

  -상관관계가 없는 경우